三、解答题（本大题满分74 分）本大题共5 题，解答下列各题须写出必要的步骤.

19、（本题满分12 分） 本题共有2 个小题，第1 小题满分6 分，第2 小题满分6 分.

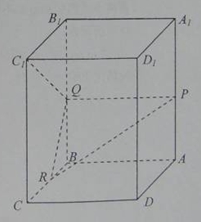
已知正四棱柱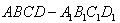，底面边长为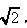，点P、Q、R分别在棱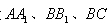上，Q 是BB1 中点，且PQ / /AB ，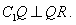

（1）求证：；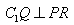

（2）若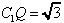，求四面体C1PQR 的体积.

20、（本题满分14 分） 本题共有2 个小题，第1 小题满分6 分，第2 小题满分8 分.

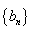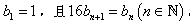已知数列满足，设数列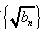的前n 项和是 .

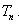（1）比较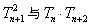的大小；

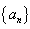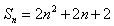（2）若数列 的前n项和，数列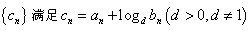 ，求d 的取值范围使得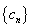是递增数列.

21、（本题满分14 分） 本题共有3 个小题，第1 小题满分5 分，第2 小题满分6 分，第3 小题满分3 分.

某种波的传播是由曲线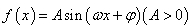来实现的，我们把函数解析式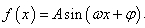称为“波”，把振幅都是A 的波称为“ A 类波”，把两个解析式相加称为波的叠加.

（1）已知“1 类波”中的两个波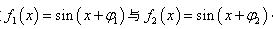叠加后仍是“1类波”，求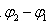的值；

（2）在“ A 类波“中有一个是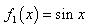，从 A类波中再找出两个不同的波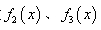，使得这三个不同的波叠加之后是平波，即叠加后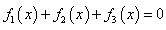，并说明理由.

（3）在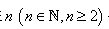个“ A类波”的情况下对（2）进行推广，使得（2）是推广后命题的一个特例. 只需写出推广的结论，而不需证明.

22、（本题满分16 分） 本题共有3 个小题，第1 小题满分4 分，第2 小题满分6 分，第3 小题满分6 分.

设函数 .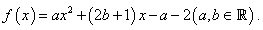

（1）若a=0，当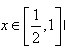时恒有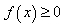，求b 的取值范围；

（2）若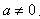且b =－1，试在直角坐标平面内找出横坐标不同的两个点，使得函数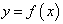的图像永远不经过这两点；

（3）若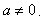，函数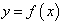在区间[3, 4]上至少有一个零点，求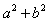的最小值.

23、（本题满分18 分） 本题共有3 个小题，第1 小题满分4 分，第2 小题满分6 分，第3 小题满分8 分.

设有二元关系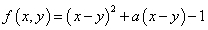，已知曲线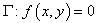

（1）若a =2时，正方形 ABCD的四个顶点均在曲线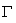上，求正方形 ABCD的面积；

（2）设曲线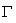与x轴的交点是M 、N ，抛物线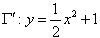与 y 轴的交点是G ，直线MG与曲线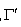交于点P，直线NG 与曲线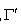交于Q，求证：直线PQ过定点，并求出该定点的坐标.

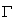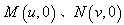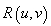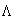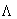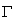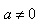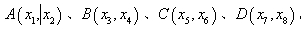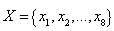（3）设曲线与x轴的交点是，可知动点在某确定的曲线上运动，曲线与上述曲线在时共有四个交点： ，集合的所

有非空子集设为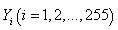，将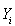中的所有元素相加（若i Y 中只有一个元素，则其是其自身）得到255 个数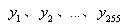，求所有的正整数n 的值，使得 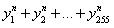是与变数a及变数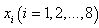均无关的常数.
数学学习  http://www.yggk.net/math/