2015丹东一模文科数学试题及答案(7)
学习频道 来源: 丹东一模 2025-02-26 大 中 小
(21)(本小题满分12分)
解:(I)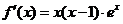 ,
,
由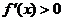 得
得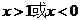 ,由
,由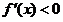 得
得 ,
,
∴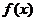 单调递增区间是
单调递增区间是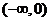 和
和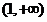 ,单调递减区间是
,单调递减区间是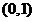 ,
,
∵函数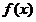 在
在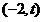 上是单调函数,
上是单调函数,
∴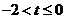 ,即
,即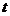 的取值范围是
的取值范围是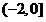 ; …………(6分)
; …………(6分)
(II)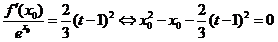 ,设
,设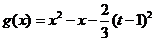 ,
,
问题转化为证明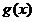 在
在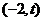 上有零点,并讨论零点的个数, …………(8分)
上有零点,并讨论零点的个数, …………(8分)
∵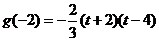 ,
, ,所以
,所以
当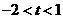 或
或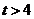 时,
时,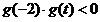 ,
,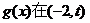 只有1个零点;
只有1个零点;
当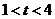 时,
时,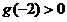 ,
,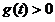 ,由于
,由于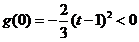 ,
,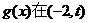 有且有2个零点;
有且有2个零点;
当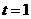 时,
时,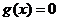 得
得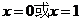 ,
,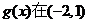 只有1个零点;
只有1个零点;
当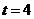 时,
时,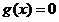 得
得 ,
,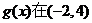 只有1个零点;
只有1个零点;
因此,对于任意的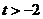 ,总存在
,总存在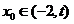 ,使得
,使得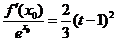 ,
,
且当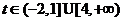 时,
时,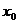 的个数是1,当
的个数是1,当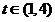 时,
时,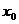 的个数是2.
的个数是2.
…………(12分)
 (23)(本小题满分10分)选修4-4:坐标系与参数方程
(23)(本小题满分10分)选修4-4:坐标系与参数方程
解:(I)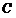 的极坐标方程化为
的极坐标方程化为 ,
,
∴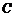 的直角坐标方程是
的直角坐标方程是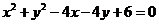 ,
,
即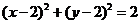 ,
,
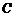 的参数方程是
的参数方程是 ,
,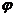 是参数; …………(5分)
是参数; …………(5分)
(II)由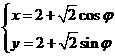 (
(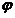 是参数)得到
是参数)得到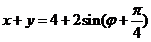
∴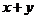 的最大值是6,最小值是2. …………(10分)
的最大值是6,最小值是2. …………(10分)
(24)(本小题满分10分)选修4-5 :不等式选讲
:不等式选讲
解:(I)当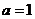 时,此不等式为
时,此不等式为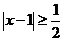 ,解得
,解得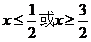 ,
,
∴不等式的解集为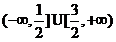 ; …………(5分)
; …………(5分)
(II)∵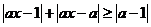 ,
,
∴原不等式解集为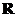 等价于
等价于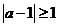 ,∵
,∵ ,∴
,∴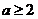 ,
,
∴实数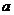 的取值范围为
的取值范围为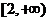 . …………(10分)
. …………(10分)