2015东城一模理科数学答案(2)
学习频道 来源: 东城一模 2025-02-26 大 中 小
第二部分(非选择题 共110分)
二、 填空题(共6小题,每小题5分,共30分)
(9)设等差数列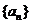 的前
的前 项和为
项和为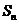 ,若
,若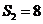 ,
,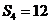 ,则
,则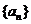 的公差
的公差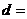 .
.
(10)曲线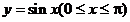 与
与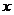 轴围成的封闭区域的面积为 .
轴围成的封闭区域的面积为 .
(11)如图,在△ 中,
中,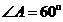 ,
,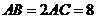 ,过
,过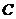 作△
作△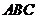 外接圆的切线
外接圆的切线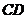 ,
,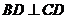 于
于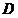 ,
,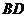 与外接圆交于点
与外接圆交于点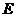 ,则
,则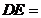 .
.
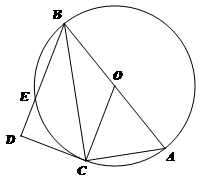
(12)已知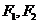 分别为椭圆
分别为椭圆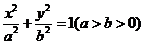 的左、右焦点,
的左、右焦点,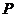 为椭圆上一点,且
为椭圆上一点,且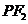 垂直于
垂直于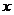 轴.若
轴.若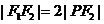 ,则该椭圆的离心率为 .
,则该椭圆的离心率为 .
(13)已知函数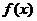 是
是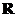 上的减函数,且
上的减函数,且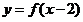 的图象关于点
的图象关于点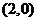 成中心对称.若
成中心对称.若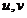 满足不等式组
满足不等式组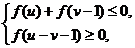 则
则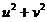 的最小值为 .
的最小值为 .
(14)已知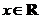 ,定义:
,定义: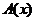 表示不小于
表示不小于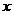 的最小整数.如
的最小整数.如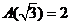 ,
,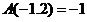 .
.
若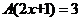 ,则
,则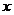 的取值范围是 ;
的取值范围是 ;
若 且
且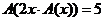 ,则
,则 的取值范围是 .
的取值范围是 .
三、解答题(共6小题,共80分。解答应写出文字说明,演算步骤或证明过程)
(15)(本小题共13分)
在△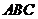 中,
中,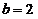 ,
,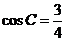 ,△
,△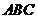 的面积为
的面积为 .
.
(Ⅰ)求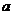 的值;
的值;
(Ⅱ)求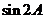 值.
值.
(16)(本小题共13分)
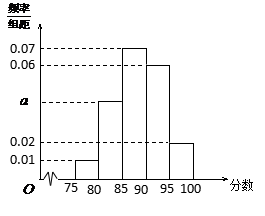 某地区有
某地区有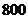 名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:
名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是: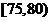 ,
,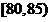 ,
,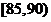 ,
,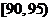 ,
,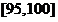 .规定
.规定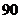 分及其以上为合格.
分及其以上为合格.

(Ⅰ)求图中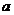 的值
的值
(Ⅱ)根据频率分布直方图估计该地区学员交通法规考试合格的概率;
(Ⅲ)若三个人参加交通法规考试,用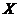 表示这三人中考试合格的人数,求
表示这三人中考试合格的人数,求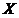 的分布列与数学期望.
的分布列与数学期望.
(17)(本小题共14分)
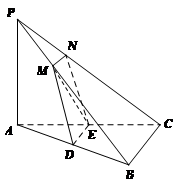 如图,在三棱锥
如图,在三棱锥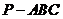 中,
中,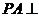 底面
底面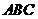 ,
,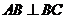 ,
,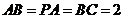 .
.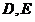 分别为
分别为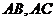 的中点,过
的中点,过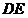 的平面与
的平面与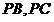 相交于点
相交于点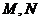 (
(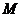 与
与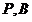 不重合,
不重合,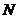 与
与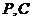 不重合).
不重合).
(Ⅰ)求证: ∥
∥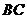 ;
;
(Ⅱ)求直线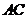 与平面
与平面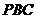 所成角的大小;
所成角的大小;
(Ⅲ)若直线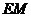 与直线
与直线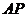 所成角的余弦值
所成角的余弦值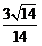 时,
时,
求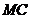 的长.
的长.
(18)(本小题共13分)
已知函数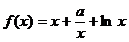 ,
,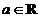 .
.
(Ⅰ)若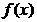 在
在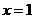 处取得极值,求
处取得极值,求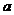 的值;
的值;
(Ⅱ)若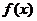 在区间
在区间 上单调递增, 求
上单调递增, 求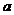 的取值范围;
的取值范围;
(Ⅲ)讨论函数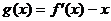 的零点个数.
的零点个数.
(19)(本小题共13分)
在平面直角坐标系中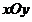 中,动点
中,动点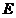 到定点
到定点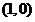 的距离与它到直线
的距离与它到直线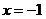 的距离相等.
的距离相等.
(Ⅰ)求动点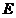 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设动直线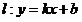 与曲线
与曲线 相切于点
相切于点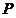 ,与直线
,与直线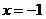 相交于点
相交于点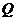 .
.
证明:以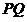 为直径的圆恒过
为直径的圆恒过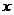 轴上某定点.
轴上某定点.
(20)(本小题共14分)
在无穷数列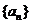 中,
中,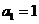 ,对于任意
,对于任意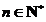 ,都有
,都有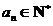 ,且
,且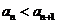 .设集合
.设集合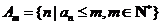 ,将集合
,将集合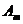 中的元素的最大值记为
中的元素的最大值记为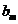 ,即
,即 是数列
是数列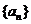 中满足不等式
中满足不等式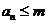 的所有项的项数的最大值,我们称数列
的所有项的项数的最大值,我们称数列 为数列
为数列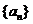 的伴随数列.
的伴随数列.
例如:数列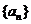 是
是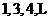 ,它的伴随数列
,它的伴随数列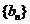 是
是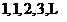 .
.
(Ⅰ)设数列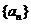 是
是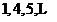 ,请写出
,请写出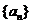 的伴随数列
的伴随数列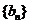 的前
的前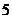 项;
项;
(Ⅱ)设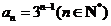 ,求数列
,求数列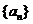 的伴随数列
的伴随数列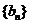 的前
的前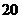 项和;
项和;
(Ⅲ)设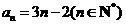 ,求数列
,求数列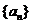 的伴随数列
的伴随数列 前
前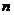 项和
项和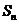 .
.
数学学习 http://www.yggk.net/math/