2015江淮十校4月联考文科数学试题答案(5)
学习频道 来源: 阳光高考信息平台 2024-07-20 大 中 小
文科数学答案
一、选择题(本大题共10小题,每小题5分,共50分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
A |
B |
D |
C |
C |
A |
A |
B |
D |
C |
二、填空题(本大题共5小题,每小题5分,共25分).
|
题号 |
11 |
12 |
13 |
14 |
15 |
|
答案 |
|
|
|
|
①③④ |
⒖【答案】①③④.
【解析】函数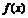 具有“自平行性”,即对定义域内的任意自变量
具有“自平行性”,即对定义域内的任意自变量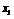 ,总存在
,总存在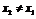 ,使得
,使得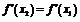 .对于①,
.对于①,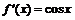 ,满足条件,故①正确;对于②,
,满足条件,故①正确;对于②,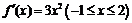 ,对任意
,对任意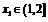 ,不存在
,不存在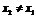 ,使得
,使得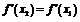 成立,故②错误;对于③,当
成立,故②错误;对于③,当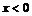 时,
时,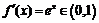 ,而
,而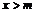 时,
时,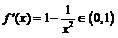 ,则
,则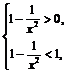 解得
解得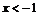 (舍去)或
(舍去)或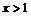 ,则
,则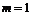 ,故③正确;对于④,
,故③正确;对于④,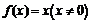 不符合定义,故④正确;对于⑤,同④,其导函数为奇函数,故⑤不正确.
不符合定义,故④正确;对于⑤,同④,其导函数为奇函数,故⑤不正确.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程. 解答写在答题卡上的指定区域内.
⒗(本小题满分12分)
解:(Ⅰ)
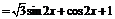
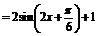 ,……………………………………………………………………4分
,……………………………………………………………………4分
故当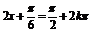 ,即
,即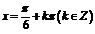 时,
时,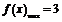 ; ……………………………………6分
; ……………………………………6分
(Ⅱ)由 ,知
,知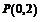 .
.
由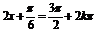 ,得
,得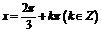 ,此时
,此时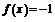 ,则
,则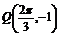 .………………………8分
.………………………8分
而由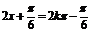 ,得
,得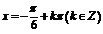 ,则
,则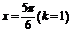 ,故
,故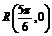 ,……………………10分
,……………………10分
从而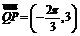 ,
,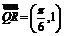 ,因此
,因此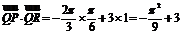 . ………………………12分
. ………………………12分
⒘(本小题满分12分)
解:(Ⅰ)设的公差为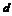 ,由题意,
,由题意,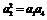 ,即
,即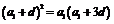 ………………………2分
………………………2分
于是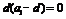
因为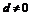 ,且
,且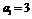 ,所以
,所以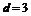 . …………………………………………………4分
. …………………………………………………4分
故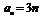 . ……………………………………………………………………5分
. ……………………………………………………………………5分
(Ⅱ)由(Ⅰ)知,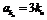 ,……………………………………………………………6分
,……………………………………………………………6分
又数列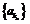 是以
是以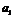 为首项,
为首项,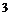 为公比的等比数列,则
为公比的等比数列,则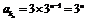 , ………7分
, ………7分
所以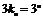 ,即
,即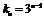 . ………………………………………………………8分
. ………………………………………………………8分
因此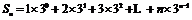 ①
①
则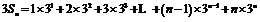 ② ……………………………………………10分
② ……………………………………………10分
由①-②得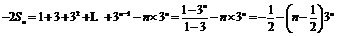
因此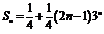 . ……………………………………………………………………12分
. ……………………………………………………………………12分
⒙(本小题满分12分)
解:(Ⅰ)由题意可知,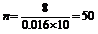 ,
,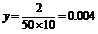 ,………………………2分
,………………………2分
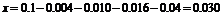 , …………………………………………………3分
, …………………………………………………3分
平均分约为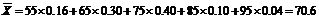 .……………………5分
.……………………5分
(Ⅱ)由题意可知,分数在[80,90)有5人,分别记为 ,分数在[90,100)有2人,分别记为F,G.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:
,分数在[90,100)有2人,分别记为F,G.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形: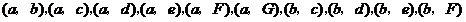 ,
,
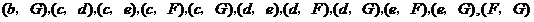 ,共有21个等可能基本事件;……………………………………………………………………………………9分
,共有21个等可能基本事件;……………………………………………………………………………………9分
其中符合“抽取的2名同学来自不同组”的基本事件有(a,F),
(a,G),(b,F),(b,G),(c,F),(c,G),(d,F),(d,G),(e,F),(e,G),共10个,……11分
所以抽取的2名同学来自不同组的概率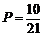 .……………………………………………………12分
.……………………………………………………12分
⒚(本小题满分13分)
(Ⅰ)证明:连结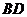 交
交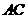 于
于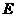 ,连结
,连结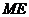 .
.
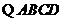 是正方形,∴
是正方形,∴ 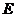 是
是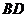 的中点.
的中点.
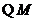 是
是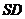 的中点,∴
的中点,∴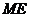 是△
是△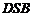 的中位线.
的中位线.
∴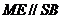 . 2分
. 2分
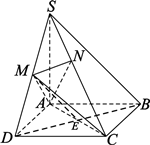 又∵
又∵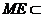 平面
平面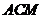 ,
,
 平面
平面 ,
,
∴
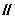 平面
平面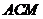 . 4分
. 4分
(Ⅱ)证明:由条件有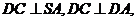
∴ 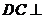 平面
平面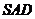 ,∴
,∴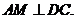 …………………………6分
…………………………6分
又∵ 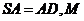 是
是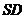 的中点,∴
的中点,∴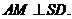
∴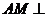 平面
平面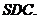 ∴
∴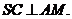 …………………………………………………8分
…………………………………………………8分
由已知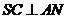 ,∴
,∴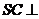 平面
平面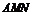 . …………………………………………………9分
. …………………………………………………9分
解:(Ⅲ)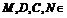 平面
平面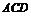 ,几何体
,几何体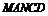 为四棱锥
为四棱锥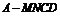 .由(Ⅱ)知
.由(Ⅱ)知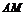 为点
为点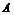 到平面
到平面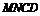 的距离. ……………………………………………………10分
的距离. ……………………………………………………10分
因为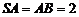 ,则
,则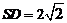 ,
,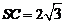 ,
, 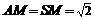 .
.
因为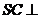 平面
平面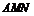 ,则
,则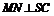 ,故
,故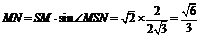 ,
,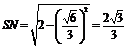 ,因此
,因此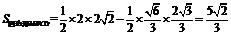 ,……………………………………………………12分
,……………………………………………………12分
则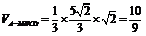 . ……………………………………………………13分
. ……………………………………………………13分
⒛(本小题满分13分)
解:(Ⅰ)由题意,得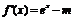 , …………………………………………………1分
, …………………………………………………1分
所以函数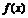 在
在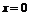 处的切线斜率
处的切线斜率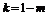 , …………………………………………………2分
, …………………………………………………2分
又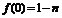 ,所以函数
,所以函数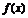 在
在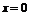 处的切线方程
处的切线方程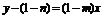 , ………………………4分
, ………………………4分
将点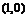 代入,得
代入,得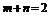 . …………………………………………………6分
. …………………………………………………6分
(Ⅱ)当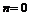 时,函数
时,函数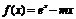 的定义域为
的定义域为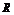 ,
,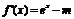 .因为
.因为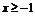 ,所以
,所以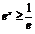 .
.
①当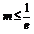 时,
时, ,函数
,函数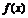 在
在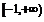 上单调递增,从而
上单调递增,从而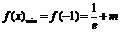 ,无最大值; …………………………………………………9分
,无最大值; …………………………………………………9分
②当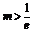 时,由
时,由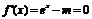 ,解得
,解得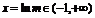 ,
,
当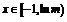 时,
时,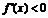 ,
,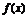 单调递减;当
单调递减;当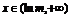 时,
时,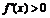 ,
,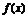 单调递增.
单调递增.
所以函数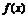 在
在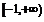 上有最小值为
上有最小值为 ,无最大值. …………………………12分
,无最大值. …………………………12分
综上知:当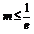 时,函数
时,函数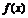 在
在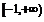 上单调递增,有最小值
上单调递增,有最小值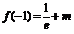 ,无最大值;
,无最大值;
当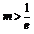 时,函数
时,函数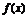 在
在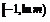 上单调递减,在
上单调递减,在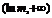 上单调递增,有最小值为
上单调递增,有最小值为 ,无最大值. …………………………………………………13分
,无最大值. …………………………………………………13分
21. (本小题满分13分)
解:(Ⅰ)抛物线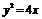 的准线为
的准线为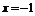 ,则
,则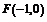 ,即
,即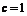 .……………………………………2分
.……………………………………2分
又点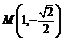 在椭圆上,则
在椭圆上,则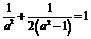 ,解得
,解得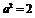 , ……………………………………4分
, ……………………………………4分
故求椭圆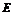 的方程为
的方程为 .………………………………………………………………………5分
.………………………………………………………………………5分
(Ⅱ)设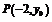 、
、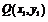 .
.
依题意可知切线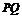 的斜率存在,设为
的斜率存在,设为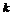 ,则
,则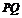 :
: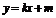 ,并代入到
,并代入到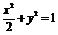 中,整理得:
中,整理得:
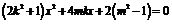 ………………………………………………………………………8分
………………………………………………………………………8分
因此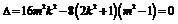 ,即
,即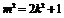 .……………………………………………9分
.……………………………………………9分
从而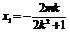 ,
,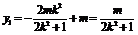 ,则
,则 ;…………………………10分
;…………………………10分
又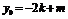 ,则
,则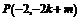 ,
,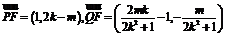 .…………………11分
.…………………11分
由于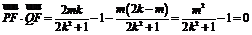 ,故
,故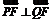 ,即
,即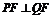 .………………13分
.………………13分