2015长春二模理科数学试题及答案(6)
学习频道 来源: 阳光高考门户-长春二模 2025-02-26 大 中 小
二、填空题(本大题包括4小题,每小题5分,共20分)
 简答与提示:
简答与提示:
13. 【命题意图】本题主要考查二项式定理的有关知识,属于基础题.
【试题解析】由题意可知常数项为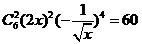 .
.
14. 【命题意图】本题考查定积分的几何意义及微积分基本定理,属于基础题.
【试题解析】由题意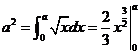 ,所以
,所以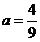 .
.
15. 【命题意图】球的内接几何体问题是高 考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.
考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.
【试题解析】由题意,面积最小的截面是以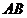 为直径,可求得
为直径,可求得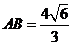 ,进而截面面积的最小值为
,进而截面面积的最小值为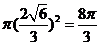 .
.
16. 【命题意图】本题主要考查数形结合以及函数的零点与交点的相关问题,需要学生对图像进行理解,对学生的能力提出很高要求,属于难题.
【试题解析】由题意可知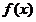 是周期为4的偶函数,对称轴为直线
是周期为4的偶函数,对称轴为直线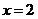 . 若
. 若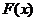 恰有4个零点,有
恰有4个零点,有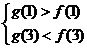 ,解得
,解得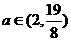 .
.
三、解答题(本大题必做题5小题,三选一选1小题,共70分)
17. (本小题满分12分)
【命题意图】本小题主要考查两角和的正切公式,以及同角三角函数的应用,并借助正弦定理考查边角关系的运算,对考生的化归与转化能力有较高要求.
【试题解析】解:(1)  (3分)
(3分)
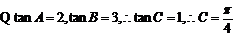 (6分)
(6分)
(2)因为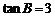
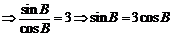 ,而
,而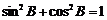 ,且
,且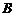 为锐角,可求得
为锐角,可求得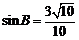 . (9分)
. (9分)
所以在△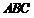 中,由正弦定理得,
中,由正弦定理得,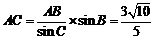 . (12分)
. (12分)
18. (本小题满分12分)
【命题意图】本小题主要考查统计与概率的相关知识、离散型随机变量的分布列以及数学期望的求法. 本题主要考查数据处理能力.
【试题解析】(1)由图可知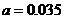 ,
,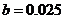 . (4分)
. (4分)
(2) 利用分层抽样从样本中抽取10人,其中属于 高消费人群的为6人,属于潜在消费人群的为4人. (6分)
高消费人群的为6人,属于潜在消费人群的为4人. (6分)
从中取出三人,并计算三人所获得代金券的总和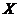 ,
,
则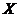 的
的 所有可能取值为:150,200,250,300.
所有可能取值为:150,200,250,300.
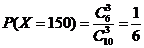 ,
, 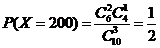 ,
,
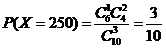 ,
, 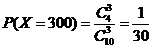 ,
,
|
|
150[来源:学*科*网Z*X*X*K] |
200 |
250 |
300 |
|
|
|
|
|
|
 (10分)
(10分)
且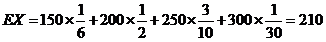 . (12分)
. (12分)
19. (本小题满分12分)
【命题意图】本小 题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用. 本小题对考生的空间想象能力与
题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用. 本小题对考生的空间想象能力与 运算求解能力有较高要求.
运算求解能力有较高要求.
【试题解析】解:(1) 取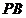 中点
中点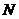 ,连结
,连结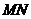 、
、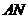 ,
,
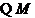 是
是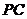 中点,
中点,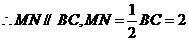 ,
,
又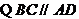 ,
,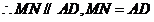 ,
,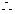 四边形
四边形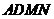 为平行四边形
为平行四边形
 ,
,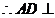 平面
平面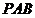 ,
,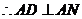 ,
,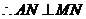
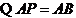 ,
,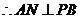 ,
,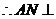 平面
平面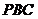 ,
,
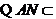 平面
平面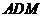 ,
,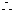 平面
平面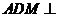 平面
平面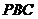 .
.  (6分
(6分 )
)
(2) 存在符合条件的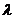 .以
.以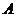 为原点,
为原点,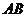 方向为
方向为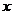 轴,
轴,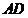 方向为
方向为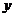 轴,
轴,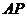 方向为
方向为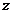 轴,建立空间直角坐标系
轴,建立空间直角坐标系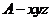 ,设
,设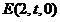 ,
,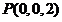 ,
,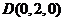 ,
,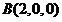
从而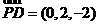 ,
,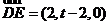 ,则平面
,则平面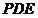 的法向量为
的法向量为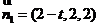 ,
,
又平面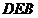 即为
即为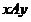 平面,其法向量
平面,其法向量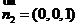 ,
,
则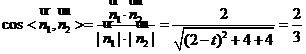 ,
,
解得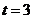 或
或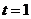 ,进而
,进而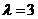 或
或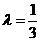 . (12分)
. (12分)
20. (本小题满分12分)
【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法,椭圆 方程的求法、直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
方程的求法、直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
【试题解析】解:(1) 已知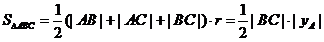 ,且
,且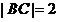 ,
,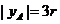 ,其中
,其中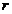 为内切圆半径,化简得:
为内切圆半径,化简得: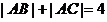 ,顶点
,顶点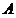 的轨迹是以
的轨迹是以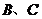 为焦点,长轴长为4的椭圆(去掉长轴端点),其中
为焦点,长轴长为4的椭圆(去掉长轴端点),其中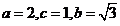
进而其方程为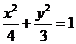
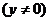 . (5分)
. (5分)
(2) 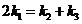 ,以下进行证明:
,以下进行证明:
当直线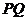 斜率存在时,设直线
斜率存在时,设直线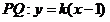 且
且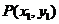 ,
,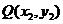 ,
,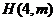
联立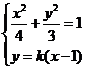 可得
可得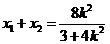 ,
,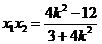 . (8分)
. (8分)
由题意: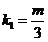 ,
,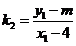 ,
,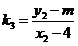 .
.

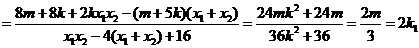
当直线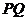 斜率不存在时,
斜率不存在时,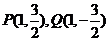 ,
,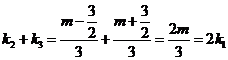
综上可得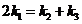 . (12分)
. (12分)
21. (本小题满分12分)
【命题意图】本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值以及函数零点的情况. 本小题对考生的逻辑推理能力与运算求解有较高要求.
【试题解析】解 :(1) 对
:(1) 对 求导得:
求导得: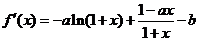 ,根据条件知
,根据条件知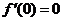 ,所以
,所以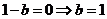 . (3分)
. (3分)
(2) 由(1)得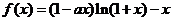 ,
,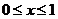
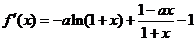
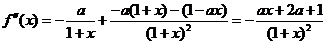 .
.
① 当 时,由于
时,由于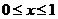 ,有
,有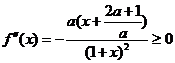 ,于是
,于是 在
在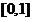 上单调递增,从而
上单调递增,从而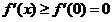 ,因此
,因此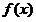 在
在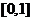 上单调递增,即
上单调递增,即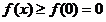 而且仅有
而且仅有
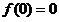 ;
;
②当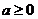 时,由于
时,由于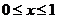 ,有
,有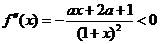 ,于是
,于是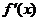 在
在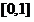 上单调递减,从而
上单调递减,从而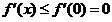 ,因此
,因此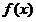 在
在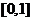 上单调递减,即
上单调递减,即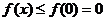 而且仅有
而且仅有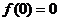 ;
;
③当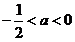 时,令
时,令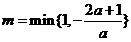 ,当
,当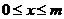 时,
时,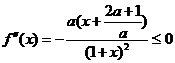 ,于是
,于是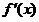 在
在 上单调递减,从而
上单调递减,从而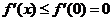 ,因此
,因此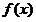 在
在 上单调递减,
上单调递减,
即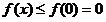 而且仅有
而且仅有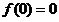 .
.
综上可知,所求实数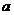 的取值范围是
的取值范围是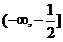 . (8分)
. (8分)
数学学习 http://www.yggk.net/math/