2015长春二模理科数学试题及答案(7)
学习频道 来源: 阳光高考门户-长春二模 2025-02-26 大 中 小
(3) 对要证明的不等式等价变形如下:
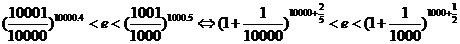
所以可以考虑证明:对于任意的正整数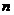 ,不等式
,不等式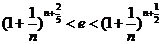 恒成立. 并且继续作如下等价变形
恒成立. 并且继续作如下等价变形
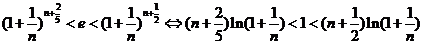
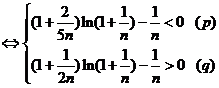
对于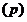 相当于(2)中
相当于(2)中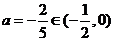 ,
,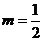 情形,有
情形,有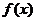 在
在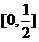 上单调递减,即
上单调递减,即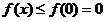 而且仅有
而且仅有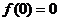 .
.
取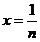 ,当
,当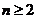 时,
时,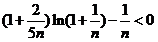 成立;
成立;
当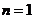 时,
时,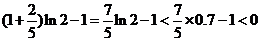 .
.
从而对于任意正整数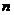 都有
都有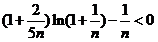 成立.
成立.
对于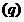 相当于(2)中
相当于(2)中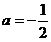 情形,对于任意
情形,对于任意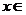
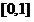 ,恒有
,恒有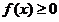 而且仅有
而且仅有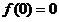 . 取
. 取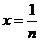 ,得:对于任意正整数
,得:对于任意正整数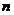 都有
都有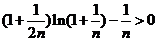 成立.
成立.
因此对于任意正整数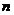 ,不等式
,不等式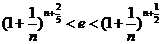 恒成立.
恒成立.
这样依据不等式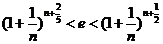 ,再令
,再令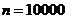 利用左边,令
利用左边,令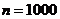 利用右边,即可得到
利用右边,即可得到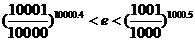 成立. (12分)
成立. (12分)
22. (本小题满分10分)[来源:Z*xx*k.Com]
【命题意图】本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形 相似等内容. 本小题重点考查考生对平面几何推理能力.
【试题解析】解:(1) 由题意可知,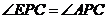 ,
,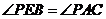 ,
,
则△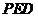 ∽△
∽△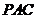 ,则
,则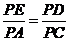 ,又
,又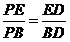 ,则
,则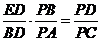 . (5分)
. (5分)
(2) 由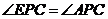 ,
,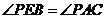 ,可得
,可得 ,
,
在△ 中,
中,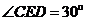 ,可知
,可知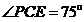 . (10分)
. (10分)
23. (本小题满分10分)
【命题意图】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、利用直线的参数方程的几何意义求解直线与曲线交点的距离等内容. 本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求.
【试题解析】解:(1) 对于曲线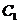 有
有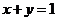 ,对于曲线
,对于曲线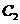 有
有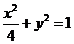 .(5分)
.(5分)
(2) 显然曲线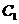 :
: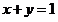 为直线,则其参数方程可写为
为直线,则其参数方程可写为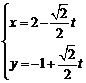 (
(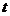 为参数)与曲线
为参数)与曲线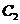 :
: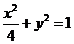 联立,可知
联立,可知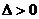 ,所以
,所以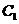 与
与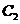 存在两个交点,
存在两个交点,
由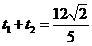 ,
,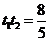 ,得
,得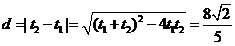 . (10分)
. (10分)
