2015大连一模理科数学试题及答案(8)
学习频道 来源: 大连一模 2025-02-26 大 中 小
解法2. 当斜率存在时,设切线方程为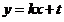 ,联立方程:
,联立方程:
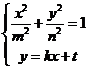 可得
可得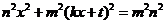 ,化简可得:
,化简可得:
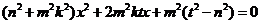 ,①
,①
由题可得: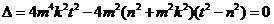 , ……… 4分
, ……… 4分
化简可得: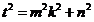 ,
,
①式只有一个根,记作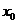 ,
,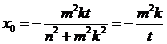 ,
,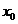 为切点的横坐标,
为切点的横坐标,
切点的纵坐标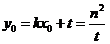 ,所以
,所以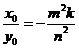 ,所以
,所以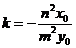 ,
,
所以切线方程为: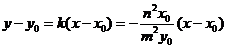 ,
,
化简得: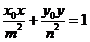 . ……… 6分
. ……… 6分
当切线斜率不存在时,切线为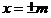 ,也符合方程
,也符合方程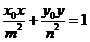 ,
,
综上: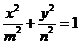 在点
在点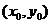 处的切线方程为
处的切线方程为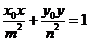 .
.
(其它解法可酌情给分,如用隐函数求导也可以)……… 7分
(Ⅲ)设点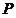
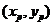 为圆
为圆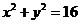 上一点,
上一点, 是椭圆
是椭圆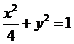 的切线,切点
的切线,切点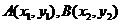 ,过点
,过点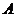 的椭圆的切线为
的椭圆的切线为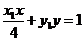 ,过点
,过点 的椭圆的切线为
的椭圆的切线为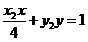 .
.
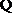 两切线都过
两切线都过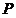 点,
点,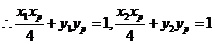 .
.
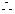 切点弦
切点弦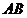 所在直线方程为
所在直线方程为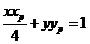 .……… 9分
.……… 9分
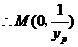 ,
,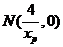 ,
,
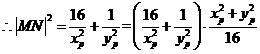
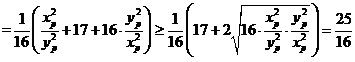 .
.
当且仅当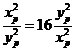 ,即
,即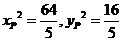 时取等,
时取等,
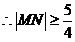 ,
,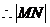 的最小值为
的最小值为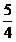 .……… 12分
.……… 12分
(21)(本小题满分12分)
解:(Ⅰ)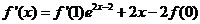 ,所以
,所以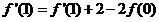 ,
,
即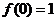 .……… 2分
.……… 2分
又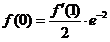 ,所以 ,所以
,所以 ,所以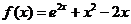 .……… 3分
.……… 3分
(Ⅱ)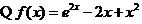 ,
,
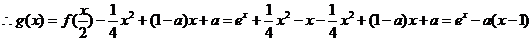 .……………4分
.……………4分
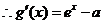 ,
,
① 时,
时,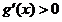 ,函数
,函数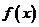 在
在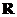 上单调递增; .……………5分
上单调递增; .……………5分
②当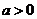 时,由
时,由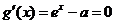 得
得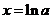 ,
,
∴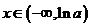 时,
时,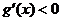 ,
, 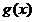 单调递减;
单调递减; 时,
时,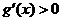 ,
,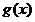 单调递增.
单调递增.
综上,当 时,函数
时,函数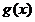 的单调递增区间为
的单调递增区间为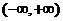 ;当
;当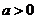 时,函数
时,函数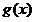 的单调递增区间为
的单调递增区间为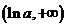 ,单调递减区间为
,单调递减区间为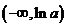 . ……………7分
. ……………7分
(Ⅲ)解:设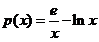 ,
,
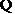
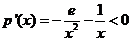 ,
,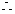
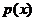 在
在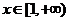 上为减函数,又
上为减函数,又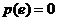 ,
,
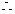 当
当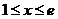 时,
时,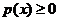 ,当
,当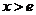 时,
时,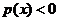 . ……………8分
. ……………8分
令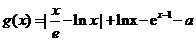 ,当
,当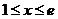 时,
时,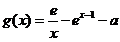 ,
,
则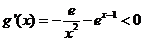 ,
,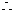
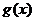 在
在 上为减函数,
上为减函数,
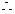
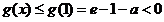 ,……………10分
,……………10分
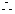
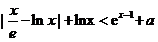 .
.
②当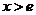 时,
时,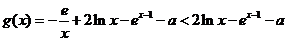 ,
,
设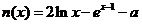 ,则
,则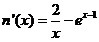 ,
,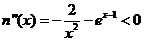 ,
,
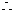
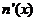 在
在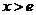 时为减函数,
时为减函数,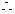
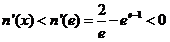 ,
,
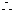
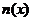 在
在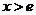 时为减函数,
时为减函数,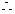
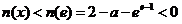 ,
,
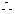
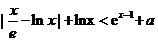 . …………… 12分
. …………… 12分
(22) 解: (Ⅰ)连接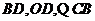 是圆
是圆 的切线,
的切线,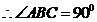 ,
,
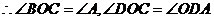 , ……………2分
, ……………2分
∵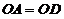 ,
,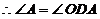 ,
,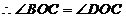 ,
,
∵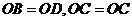 , ……………4分
, ……………4分
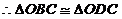 ,
,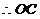 平分
平分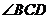 . …………… 5分
. …………… 5分
(Ⅱ)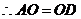 ,
, 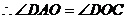 ,
,
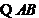 是直径,
是直径, 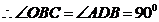 .……………7分
.……………7分
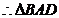 ∽
∽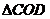 ,
,
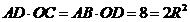 .……………9分
.……………9分
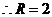 . …………… 10分
. …………… 10分
(23)解:(Ⅰ)圆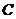 的参数方程为
的参数方程为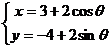 (
(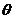 为参数)
为参数)
所以普通方程为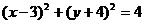 . ……………2分
. ……………2分
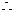 圆
圆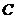 的极坐标方程:
的极坐标方程: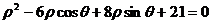 . ……………5分
. ……………5分
(Ⅱ)点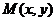 到直线
到直线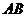
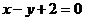 的距离为……………6分
的距离为……………6分
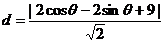 ……………7分
……………7分
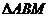 的面积
的面积 |
|
……………9分
所以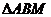 面积的最大值为
面积的最大值为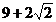 ……………10分
……………10分
(24) 解:(Ⅰ)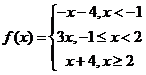 ,……………2分
,……………2分
当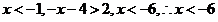
当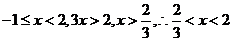
当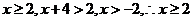
综上所述 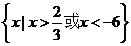 .……………5分
.……………5分
(Ⅱ)易得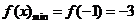 ,若
,若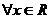 ,
,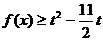 恒成立,
恒成立,
则只需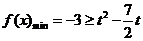 ,……………7分
,……………7分
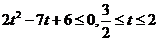 .
.
综上所述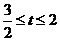 . ……………10分
. ……………10分