2015眉山二诊文科数学试卷答案(5)
学习频道 来源: 眉山二诊 2025-02-26 大 中 小
眉山市高中2015届第二次诊断性考试
数学(文史类)参考答案
一、选择题:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
C |
D |
D |
B |
B |
A |
C |
D |
A |
B |
二、填空题:
|
11. |
12. |
13. |
14. |
15. |
|
2 |
512+32 |
|
8 |
①③④ |
三、解答题:
16. 解:(1)由表可知,样本容量为n,
由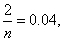 得n=50 2分
得n=50 2分
由x=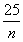 =0.5 3分
=0.5 3分
y=50-3-6-25=14 4分
z=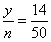 =0.28 5分
=0.28 5分
(1) 设样本视力在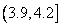 的3人为
的3人为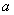 ,
,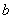 ,
,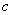 ,样本视力在
,样本视力在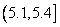 的2人为d,e.
的2人为d,e.
由题意从5人中任取两人的基本事件空间为:
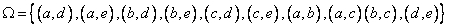
∴ ,且各个基本事件是等可能发生的。 8分
,且各个基本事件是等可能发生的。 8分
设事件A表示“抽取的两人的视力差的绝对值低于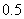 ”
”
则事件A包含的基本事件有: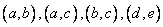
∴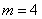
 10分
10分
∴
故抽取的两人的视力差的绝对值低于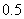 的概率为
的概率为 12分
12分
17. 解析 (1)f(x)=2sin2ωx-2(cos2ωx+1)
=sin(2ωx-6)-2, 2分
由f(x)的周期T=2ω=2,得ω=2, 4分
∴f(x)=sin(4x-6)-2,
由2kπ-2≤4x-6≤2kπ+2(k∈Z),
得-12+2≤x≤6+2(k∈Z),即f(x)的单调递增区间是
[-12+2,6+2](k∈Z). 6分
(2)由题意,得cosx=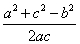 ≥
≥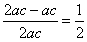
又∵0<x<π,∴0<x≤3, 8分
∴-6<4x-6≤6,
∴-2<sin(4x-6)≤1,
∴-1<sin(4x-6)-2≤2,
∴f(x)的值域为(-1,2]. 12分
18.解(1)因为{ }为等差数列,设{
}为等差数列,设{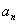 }的公差为d (d≠0),
}的公差为d (d≠0),
所以S1=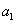 ,S2=2
,S2=2 +d,S4=4
+d,S4=4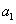 +6d.
+6d.
因为S1,S2,S4成等比数列且设其公比为q,
所以S1·S4=S2.
所以a1(4a1+6d)=(2a1+d)2.所以2a1d=d2.
因为公差d≠0.所以d=2a1.
所以q=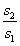 =
=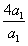 =4. 4分
=4. 4分
(2)因为S2=4,所以2a1+d=4.
又d=2a1,所以a1=1,d=2.所以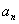 =2n-1. 6分
=2n-1. 6分
因为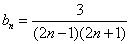 =2(2n-1-2n+1), 8分
=2(2n-1-2n+1), 8分
所以Tn=2[(1-3)+(3-5)+ +(2n-1-2n+1)]=2(1-2n+1)< 2. 10分
+(2n-1-2n+1)]=2(1-2n+1)< 2. 10分
要使Tn<20对所有n∈N*都成立,
则有20≥2,即m≥30.
因为m∈N*,所以m的最小值为30.  12分
12分
19、(Ⅰ)证明:在正方形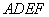 中,
中,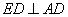 .
.
因为平面
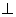 平面
平面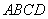 ,且平面
,且平面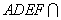 平面
平面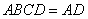 ,
,
所以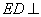 平面
平面 .
.
所以 . 2分
. 2分
在直角梯形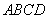 中,
中,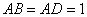 ,
,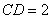 ,可得
,可得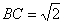 .
.
在△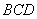 中,
中,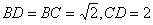 ,
,
所以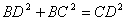 .
.
所以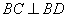 . 4分
. 4分
因为,ED、BD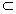 平面EBD,ED
平面EBD,ED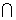 BD=D
BD=D
所以,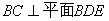 6分
6分
(Ⅱ)解:因为,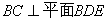 ,
,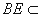 平面
平面 ,所以
,所以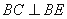
7分
所以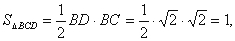
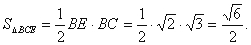 9分
9分
又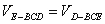 ,设点
,设点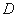 到平面
到平面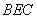 的距离为
的距离为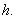
则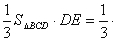 ,所以
,所以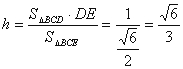 12分
12分
数学学习 http://www.yggk.net/math/