2015眉山二诊文科数学试卷答案(6)
学习频道 来源: 眉山二诊 2024-07-20 大 中 小
20、解:(Ⅰ)设椭圆的右焦点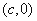
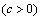 ,由右焦点到直线
,由右焦点到直线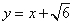 的距离为
的距离为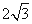 ,
,
解得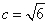 ;又由椭圆的离心率为
;又由椭圆的离心率为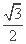 ,
,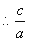
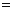
 ,解得
,解得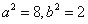 ,
,
所以椭圆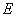 的方程为
的方程为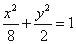 4分
4分
(Ⅱ) ①若直线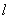 过椭圆的左顶点,则直线的方程是
过椭圆的左顶点,则直线的方程是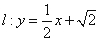 ,
,
联立方程组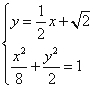 ,解得
,解得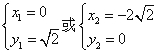 ,
,
故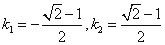 . 8分
. 8分
②猜测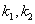 的关系是:
的关系是: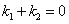 ;证明如下:
;证明如下:
设直线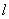 的方程为
的方程为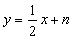
联立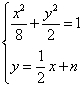 消去
消去 得
得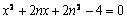
设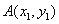 、
、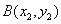 ,则
,则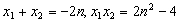 .
.
又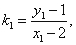
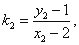 11分
11分
故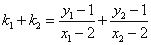
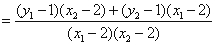 .
.
又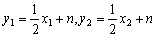 ,
,
所以上式分子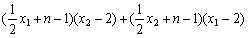
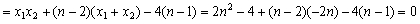 ,
,
故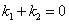 . 13分
. 13分
21、解:(Ⅰ)由题意知函数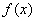 的定义域为
的定义域为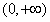 ,
,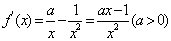 .
.
1分
由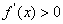 ,解得
,解得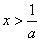 ,所以函数
,所以函数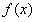 的单调增区间是
的单调增区间是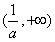 ;
;
由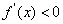 ,解得
,解得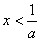 ,所以函数
,所以函数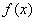 的单调减区间是
的单调减区间是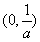 ; …………2分
; …………2分
所以,当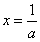 时,函数
时,函数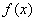 有极小值为
有极小值为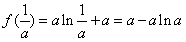 . …4分
. …4分
(Ⅱ)设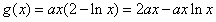 ,则函数
,则函数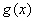 的定义域为
的定义域为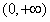 .
.
所以,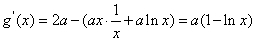 . 5分
. 5分
由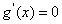 解得
解得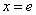 ,由
,由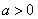 可知,当
可知,当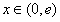 时,
时,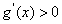 ,函数
,函数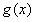 单调
单调
递增;当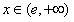 时,
时,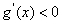 ,函数
,函数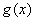 单调递减.
单调递减.
所以,函数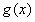 的最大值为
的最大值为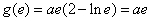 . 7分
. 7分
要使不等式恒成立,只需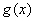 的最大值不大于1即可,即
的最大值不大于1即可,即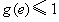 ,
,
也就是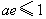 ,解得
,解得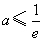 ,
,
又因为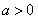 ,所以
,所以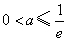 ,故
,故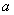 的取值范围为
的取值范围为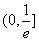 . 8分
. 8分
(Ⅲ)由(Ⅰ)可知,当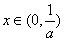 时,函数
时,函数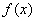 的单调递减;当
的单调递减;当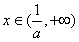 时,函数
时,函数
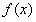 的单调递增; 9分
的单调递增; 9分
①若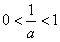 ,即
,即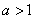 时,函数
时,函数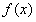 在
在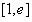 上为增函数,故函数
上为增函数,故函数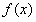 的最小值为
的最小值为
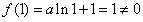 ,故不满足条件; 10分
,故不满足条件; 10分
②若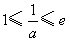 ,即
,即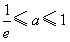 时,函数
时,函数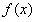 在
在 上为减函数,在
上为减函数,在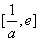 上为增函数,故函数
上为增函数,故函数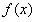 的最小值为
的最小值为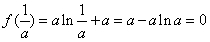 ,解得
,解得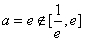 ,故不满足条件; 11分
,故不满足条件; 11分
③若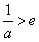 ,即
,即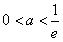 时,函数
时,函数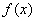 在
在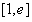 上为减函数,故函数
上为减函数,故函数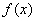 的最小值为
的最小值为 ,解得
,解得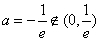 ,故不满足条件; 13分
,故不满足条件; 13分
综上所述,这样的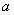 不存在. 14分
不存在. 14分