宿州市2016届高三第三次教学质量检测文科数学试题及答案(7)
学习频道 来源: 阳光高考门户 宿州三模 2025-02-26 大 中 小
2016届宿州市高三第三次教学质量检测
数学文科参考答案
一、选择题(每题5分,共60分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | A | D | C | B | C | B | D | B | A | C | C | D |
二、填空(每题5分,共20分)
13. 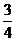 14. 91 15.
14. 91 15. 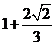 16. +1
16. +1
三、解答
17. 解 (1) 解:设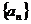 的公差d,则
的公差d,则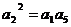 ,即
,即
∴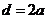 1 又
1 又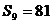 , ∴
, ∴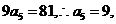 得
得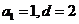
∴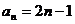 ---------------6分
---------------6分
(2)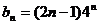
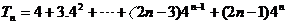
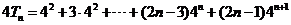

∴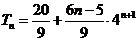
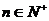 ---------------12分
---------------12分
18. 解 解 (1)由已知得,样本中有25周岁以上组工人60名,25周岁以下组工人40名.所以,样本中日平均生产件数不足60件的工人中,25周岁以上组工人有60×0.05=3(人),记为A1,A2,A3;25周岁以下组工人有40×0.05=2(人),记为B1,B2.
从中随机抽取2名工人,所有可能的结果共有10种,即:
(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
其中,至少有一名“25周岁以下组”工人的可能结果共有7种,即:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
故所求的概率为P=10. -------------6分
(2)由频率分布直方图可知,在抽取的100名工人中,“25周岁以上组”中的生产能手60×0.25=15(人),“25周岁以下组”中的生产能手40×0.375=15(人),因此可列2×2的列联表如下:
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | 15 | 45 | 60 |
25周岁以下组 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
所以得χ2=(a+b)(c+d)(a+c)(b+d)
=60×40×30×70=14≈1.786. 因为1.786<2.706.
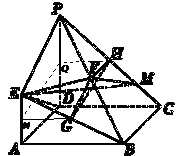 所以没有90%的把握认为“生产能手与工人所在的年龄组有关”. -------------12分
所以没有90%的把握认为“生产能手与工人所在的年龄组有关”. -------------12分
19 .(1) 证明取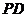 中点
中点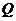 ,
, 中点
中点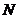 ,
,
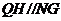 ,且
,且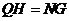 ,
,
所以四边形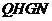 为平行四边形(如图),
为平行四边形(如图),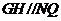 ,
,
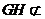 平面
平面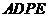 ,
,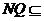 平面
平面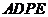 ,
,
故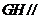 平面
平面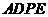
方法2:因为FH∥BC. BC∥AD,所以FH∥AD,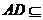 平面
平面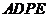 ,
,
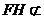 平面
平面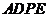 , 所以
, 所以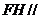 平面
平面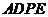 同理
同理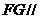 平面
平面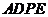 又因为
又因为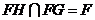 ,所以平面
,所以平面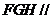 平面
平面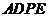 ,
,
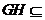 平面
平面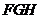
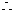
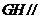 平面ADPE ------6分
平面ADPE ------6分
(2) 解 在线段PC上存在一点M,使PB⊥平面EFM.
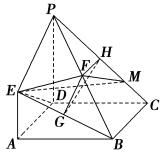 证明如下:
证明如下:
如图,在PC上取一点M,连接EF,EM,FM.
在直角三角形AEB中,因为AE=1,AB=2,
所以BE=.
在直角梯形EADP中,因为AE=1,AD=PD=2,
所以PE=,所以PE=BE.又F为PB的中点,
所以EF⊥PB. 要使PB⊥平面EFM,只需使PB⊥FM.
因为PD⊥平面ABCD,所以PD⊥CB,又CB⊥CD,PD∩CD=D,
所以CB⊥平面PCD,而PC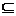 平面PCD,所以CB⊥PC.
平面PCD,所以CB⊥PC.
若PB⊥FM,则△PFM∽△PCB,可得PB=PC.
由已知可求得PB=2,PF=,PC=2,所以PM=2. ----------12分
20.解:(1)设点M点的坐标是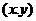 ,根据题意:
,根据题意: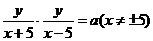
化简: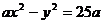 ----------2分
----------2分
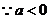
(ⅰ)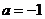 时,方程为
时,方程为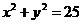 ,表示的曲线是圆(除去点
,表示的曲线是圆(除去点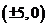 )
)
(ⅱ)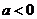 且
且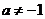 时,方程为
时,方程为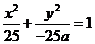 ,表示的曲线是椭圆,(除去点
,表示的曲线是椭圆,(除去点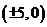 )
)
----------4分
(2)  M的轨迹方程是:
M的轨迹方程是: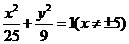
设P、Q坐标分别是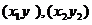
设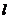 的方程:
的方程: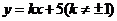 ,(
,(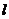 重合于y轴时不符)
重合于y轴时不符)
由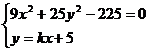 可得:
可得: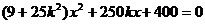
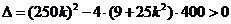 得
得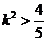
∴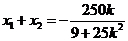 ,
,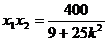 ---------8分
---------8分
∴PQ的中点坐标: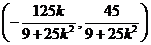
故中垂线方程: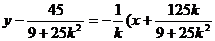 )
)
令 得
得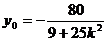
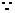
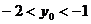 即
即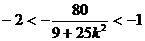
又因为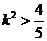 且
且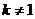 故解得
故解得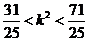 ,得
,得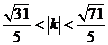
即 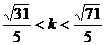 或
或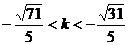
故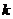 的取值范围是
的取值范围是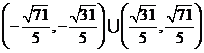 ----------12分
----------12分
21. (1) 切线的斜率
切线的斜率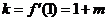 ,
,
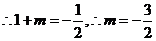 ----------3分
----------3分
(2) 由题意,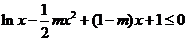 ,
,
设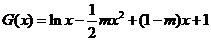 ,
,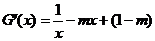 .
.
① 当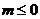 时,因为
时,因为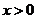 ,所以
,所以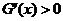 ,所以
,所以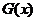 在
在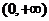 上是单调递增函数,
上是单调递增函数,
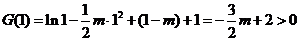 ,
,
所以关于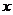 的不等式
的不等式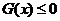 不能恒成立 ----------6分
不能恒成立 ----------6分
②当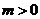 时,
时,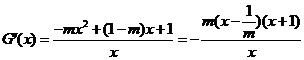
令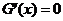 ,因为
,因为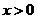 ,得
,得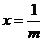 ,
,
所以当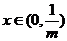 时,
时,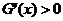 ,当
,当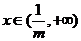 时,
时,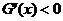
因此函数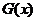 在
在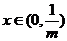 是增函数,在
是增函数,在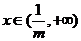 是减函数,----------9分
是减函数,----------9分
故函数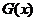 的最大值为:
的最大值为: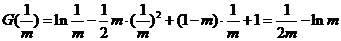
令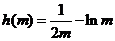 ,因为
,因为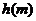 在
在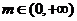 上是减函数,
上是减函数,
又因为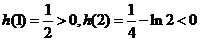 ,所以当
,所以当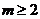 时,
时,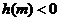 ,
,
故整数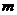 的最小值为
的最小值为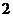 ----------12分
----------12分