2015资阳三模理科数学答案(2)
学习频道 来源: 资阳三模 2025-02-26 大 中 小
注意事项:
必须使用0.5毫米黑色墨迹签字笔在答题卡上题目指示的答题区域内作答。作图时可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚。答在试题卷、草稿纸上无效。
第Ⅱ卷共11小题。
二、填空题:本大题共5小题,每小题5分,共25分。
11.已知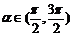 ,
,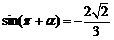 ,则
,则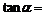 _________.
_________.
12.函数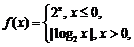 则使
则使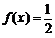 的x值的集合是___________.
的x值的集合是___________.
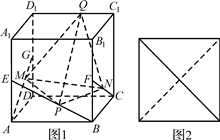 13.已知P为抛物线
13.已知P为抛物线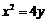 上的动点,点P在x轴上的射影为M,点A的坐标是
上的动点,点P在x轴上的射影为M,点A的坐标是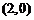 ,则
,则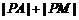 的最小值为__________.
的最小值为__________.
14.如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1Cl D1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、 CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点P到QMN的距离为__________.
15.已知8个非零实数a1,a2,a3,a4,a5,a6,a7,a8,向量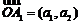 ,
,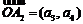 ,
,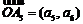 ,
,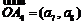 ,给出下列命题:
,给出下列命题:
①若a1,a2,…,a8为等差数列,则存在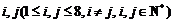 ,使
,使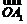 +
+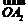 +
+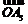 +
+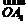 与向量
与向量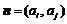 共线;
共线;
②若a1,a2,…,a8为公差不为0的等差数列,向量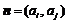
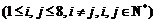 ,
,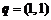 ,
,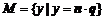 ,则集合M的元素有12个;
,则集合M的元素有12个;
③若a1,a2,…,a8为等比数列,则对任意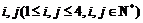 ,都有
,都有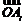 ∥
∥ ;
;
④若a1,a2,…,a8为等比数列,则存在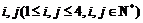 ,使
,使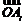 ·
·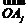 <0;
<0;
⑤若m=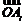 ·
·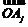
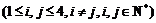 ,则m的值中至少有一个不小于0.
,则m的值中至少有一个不小于0.
其中所有真命题的序号是________________.
三、解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题满分12分)
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查.活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
|
年龄(岁) |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70] |
|
频数 |
m |
n |
15 |
10 |
7 |
3 |
|
知道的人数 |
4 |
6 |
12 |
6 |
3 |
2 |
表中所调查的居民年龄在[ 10,20),[20,30),[30,40)的人数成等差数列.
10,20),[20,30),[30,40)的人数成等差数列.
(Ⅰ)求上表中的m,n值,若从年龄在[20,30)的居民中随机选取两人,求这两人至少有一人知道灭火器使用方法的概率;
(Ⅱ)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取2人参加消防知识讲座,记选中的4人中不知道灭火器使用方法的人数为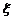 ,求随机变量
,求随机变量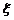 的分布列和数学期望.
的分布列和数学期望.
17.(本小题满分12分)
已知向量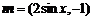 ,
,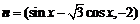 ,函数
,函数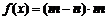 .
.
(Ⅰ)求 在区间
在区间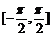 上的零点;
上的零点;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c, 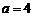 ,△ABC的面积
,△ABC的面积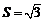 ,当x=A时,函数
,当x=A时,函数 取得极大值,求
取得极大值,求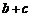 的值.
的值.
18.(本小题满分12分)
已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn=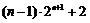 (
(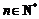 ).
).
(Ⅰ)若{bn }是首项为1,公比为2的等比数列,求数列{an}的前n项和Sn;
(Ⅱ)若{an}是等差数列,且an≠0,问:{bn}是否是等比数列?若是,求{an}和{bn}的通项公式;若不是,请说明理由.
英语学习 http://www.yggk.net/english/