2015资阳三模理科数学答案(5)
学习频道 来源: 资阳三模 2025-02-26 大 中 小
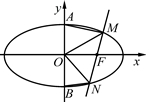 联立
联立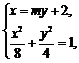 消去x,得
消去x,得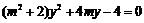 ,
,
则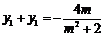 ,
,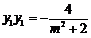 ,
,
所以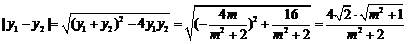 ,
,
由于M,N均在y轴右侧,则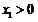 ,
,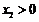 ,且
,且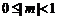 ,
,
则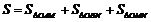
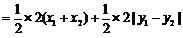
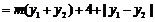
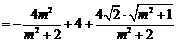
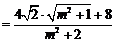 , 8分
, 8分
令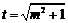 ,则
,则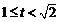 ,则
,则
【或利用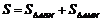 求面积S,解法如下:
求面积S,解法如下:
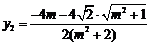 ,则
,则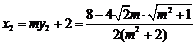 ,
,
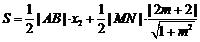
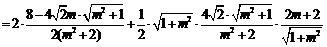
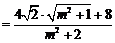 . 8分】
. 8分】
方法一、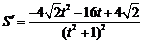
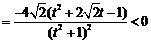 ,
,
故面积函数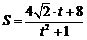 在单调递减,所以
在单调递减,所以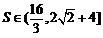 ,
,
所以面积S的取值范围是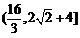 .
.
方法二、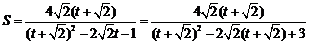
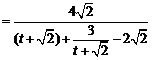 ,
,
因为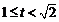 ,则
,则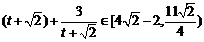 ,
,
所以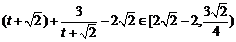 ,
,
则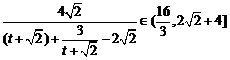 ,即
,即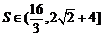 ,
,
所以面积S的取值范围是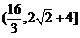 . 13分
. 13分
21.(本小题满分14分)
解析:(Ⅰ)当a=2时,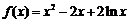 ,
,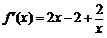 ,
,
则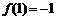 ,
,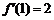 ,所以切线方程为
,所以切线方程为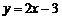 . 4分
. 4分
(Ⅱ)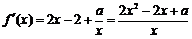 (
(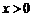 ),令
),令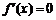 ,得
,得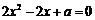 ,
,
(1)当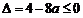 ,即
,即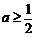 时,
时,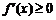 ,函数
,函数 在
在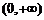 上单调递增;
上单调递增;
(2)当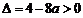 ,即
,即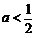 时,由
时,由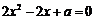 ,得
,得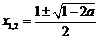 ,
,
①若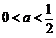 ,由
,由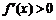 ,得
,得 或
或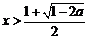 ;由
;由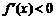 ,得
,得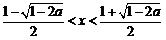 ;
;
②若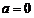 ,则
,则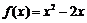 ,函数
,函数 在
在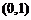 上递减,在
上递减,在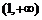 上递增;
上递增;
③若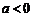 ,则函数
,则函数 在
在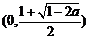 上递减,在
上递减,在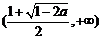 上递增.
上递增.
综上,当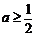 时,
时, 的单调递增区间是
的单调递增区间是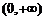 ;
;
当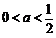 时,
时, 的单调递增区间是
的单调递增区间是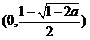 ,
,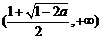 ;单调递减区间是
;单调递减区间是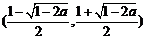 ;
;
当 时,
时, 的单调递增区间是
的单调递增区间是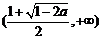 ,单调递减区间是
,单调递减区间是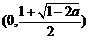 .
.
9分
(Ⅲ)由(Ⅱ)可知,函数 有两个极值点
有两个极值点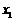 ,
, 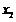 ,则
,则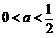 ,
,
由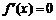 ,得
,得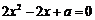 ,则
,则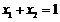 ,
,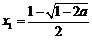 ,
,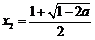 ,
,
