2015江西省八所重点中学高三4月联考理科数学试题及答案(2)
学习频道 来源: 江西省八所重点中学 2025-02-26 大 中 小
二、填空题(本题共4个小题,每小题5分,共20分)
13.计算: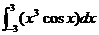 = .
= .
14.已知点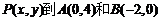 的距离相等,则
的距离相等,则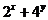 的最小值为 .
的最小值为 .
 15.如图,圆
15.如图,圆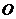 与
与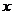 轴的正半轴的交点为
轴的正半轴的交点为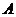 ,点
,点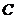 、
、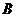 在圆
在圆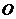 上,
上,
且点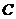 位于第一象限,点
位于第一象限,点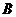 的坐标为(
的坐标为(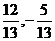 ),
),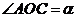 .
.
若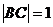 ,则
,则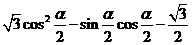 的值为 .
的值为 .
16.用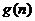 表示自然数
表示自然数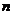 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9,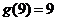 ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,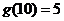 ,那么
,那么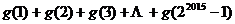 = .
= .
三、解答题(本题共6小题,共70分,解答题应写出文字说明、证明过程和演算步骤.)
17.(本小题12分)已知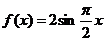 ,集合
,集合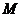 =
=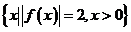 ,把
,把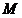 中的元素从小到大依次排成一列,得到数列
中的元素从小到大依次排成一列,得到数列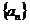 ,
,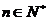 .
.
(1)求数列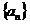 的通项公式;
的通项公式;
(2)记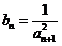 ,设数列
,设数列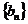 的前
的前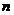 项和为
项和为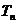 ,求证
,求证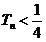 .
.
 18. (本题12分)如图,四棱锥
18. (本题12分)如图,四棱锥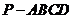 中,底面
中,底面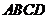 是直角梯形,
是直角梯形,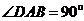 ,
,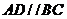 ,
,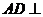 侧面
侧面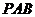 ,△
,△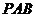 是等边三角形,
是等边三角形,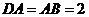 ,
, 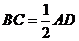 ,
,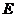 是线段
是线段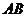 的中点.
的中点.
(1)求证: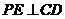 ;
;
(2)求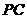 与平面
与平面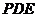 所成角的正弦值.
所成角的正弦值.
19. (本题12分)已知集合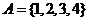 ,函数
,函数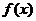 的定义域、值域都是
的定义域、值域都是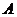 ,且对于任意
,且对于任意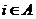 ,
,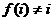 . 设
. 设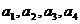 是
是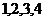 的任意一个排列,定义数表
的任意一个排列,定义数表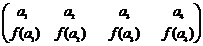 ,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表.
,若两个数表的对应位置上至少有一个数不同,就说这是两张不同的数表.
(1)求满足条件的不同的数表的张数;
(2)若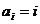 (
(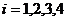 ),从所有数表中任意抽取一张,记
),从所有数表中任意抽取一张,记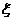 为表中
为表中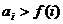 的个数,求
的个数,求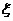 的分布列及期望.
的分布列及期望.
20.(本题12分)已知椭圆C: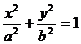 (
(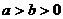 )的离心率
)的离心率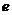 =
= ,且过点M(1,
,且过点M(1,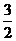 )
)
(1)求椭圆C的方程;yggk.net
(2)椭圆C长轴两端点分别为A、B,点P为椭圆上异于A、B的动点,定直线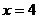 与直线PA、PB分别交于M、N两点,又E(7,0),过 E、M、N三点的圆是否过
与直线PA、PB分别交于M、N两点,又E(7,0),过 E、M、N三点的圆是否过 轴上不同于点E的定点?若经过,求出定点坐标;若不经过,请说明理由.
轴上不同于点E的定点?若经过,求出定点坐标;若不经过,请说明理由.
21. (本题12分)已知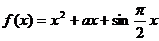
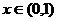
(1)若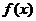 在定义域内单调递增,求
在定义域内单调递增,求 的取值范围;
的取值范围;
(2)当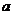 =-2时,记
=-2时,记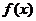 得极小值为
得极小值为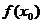 。若
。若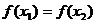 ,求证:
,求证: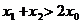 .
.
 请考生在22,23,24题中任选一题作答,如果多做,则按第一题记分
请考生在22,23,24题中任选一题作答,如果多做,则按第一题记分
22.(本小题满分10分)选修4—1:几何证明选讲.
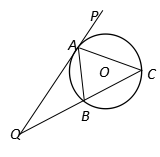
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,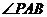 的平分线AC
的平分线AC
交⊙O于点C,连结CB,并延长与直线PQ相交于Q点,
(1)求证: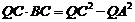 ;
;
(2)若AQ=6,AC=5.求弦AB的长.  (第22题图)
(第22题图)
23.(本小题满分10分)选修4—4:坐标系与参数方程.
在平面直角坐标系xOy中,直线l的参数方程为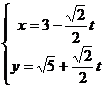 (t为参数). 在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为
(t为参数). 在以原点O为极点,x轴正半轴为极轴的极坐标中,圆C的方程为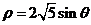 .
.
(1)写出直线l的普通方程和圆C的直角坐标方程;
(2)若点P坐标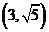 ,圆C与直线l交于A,B两点,求|PA|+|PB|的值.
,圆C与直线l交于A,B两点,求|PA|+|PB|的值.
24.(本小题满分10分)选修4—5:不等式选讲
(1)已知函数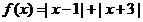 ,求x的取值范围,使
,求x的取值范围,使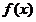 为常函数;
为常函数;
(2)若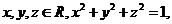 求
求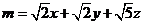 的最大值。
的最大值。
数学学习 http://www.yggk.net/math/