2015江西省八所重点中学高三4月联考理科数学试题及答案(4)
学习频道 来源: 江西省八所重点中学 2025-02-26 大 中 小
 E
E 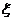 =2 ……12分
=2 ……12分
20.解:(1)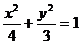 ………5分
………5分
(2)设PA,PB的斜率分别为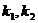 ,
,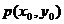 ,则
,则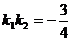 ………7分
………7分
则PA: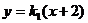 ,则
,则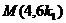
PB: 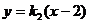 ,则
,则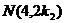
又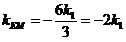 ,
,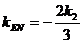
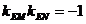 ………10分
………10分
设圆过定点F(m,o),则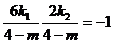 ,则m=1或m=7(舍)
,则m=1或m=7(舍)
故过点E、M、N三点的圆是以MN为直径的圆过点F(1,0)………12分
解:21.解:(1)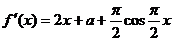
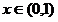
依题意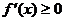 恒成立,
恒成立,
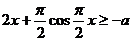
令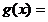
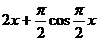
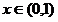
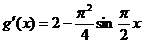
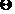
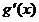 在
在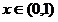 单调递减,且
单调递减,且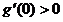 ,
,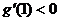
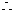
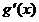 在区间
在区间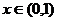 上存在唯一零点
上存在唯一零点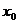 ………3分
………3分
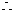
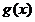 在
在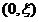 上单调递增,在
上单调递增,在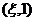 上单调递减。
上单调递减。
由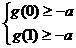 得
得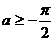 ………5分
………5分
(2)当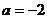 时,
时,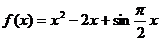
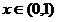
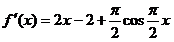 ,
,
令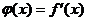
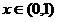
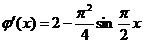 ,显然
,显然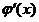 在区间
在区间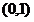 单调递减,
单调递减,
又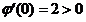 ,
,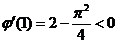
故存在唯一实数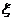 ,使得
,使得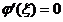
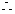
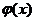 在
在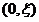 上单调递增,在
上单调递增,在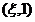 上单调递减。
上单调递减。
即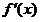 在
在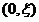 上单调递增,在
上单调递增,在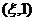 上单调递减。
上单调递减。
又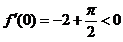 ,
,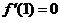
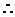
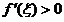 ,
,
由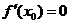 知
知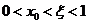 ,
,
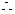
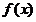 在(
在(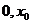 )上单调递减,在(
)上单调递减,在(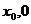 )上单调递增.
)上单调递增.
不妨设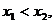 由
由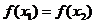 ,则
,则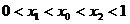
令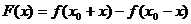 ,
,
则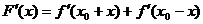 =
=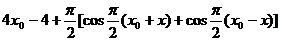
=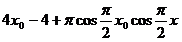 ………8分
………8分
又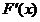 在
在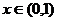 上单调递减,所以
上单调递减,所以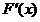 <
<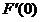 =
=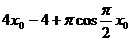 =
=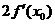 =0
=0
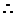
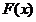 在
在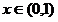 上单调递减,
上单调递减,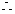
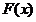 <
<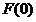 =0,即:
=0,即: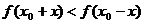
又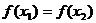 =
=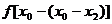 <
<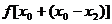 =
=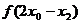 ……9分
……9分
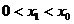
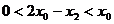
又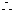
 在
在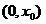 上单调递减
上单调递减
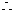
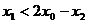
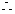
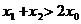 ………12分
………12分
22.(本小题满分10分)选修4—1:几何证明选讲 1
证明:(1)∵PQ与⊙O相切于点A,∴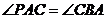
∵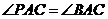 ∴
∴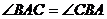
∴AC=BC=5
由切割线定理得:
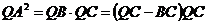
∴ 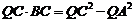 ------------5分
------------5分
(2) 由AC=BC=5,AQ=6 及(1), 知 QC=9
由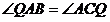 知
知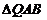 ∽
∽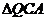
∴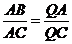 ∴
∴ 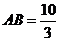 . ----------10分
. ----------10分
23.(本小题满分10分)选修4—4:坐标系与参数方程
解: (1)由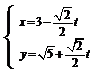 得直线l的普通方程为
得直线l的普通方程为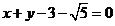 --------2分
--------2分
又由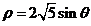 得圆C的直角坐标方程为
得圆C的直角坐标方程为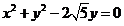
即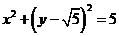 . ---------5分
. ---------5分
(2) 把直线l的参数方程代入圆C的直角坐标方程,
得 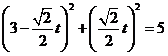 ,即
,即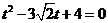
由于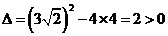 ,故可设
,故可设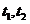 是上述方程的两实数根,
是上述方程的两实数根,
所以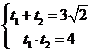 又直线l过点P
又直线l过点P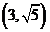 ,A、B两点对应的参数分别为
,A、B两点对应的参数分别为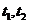
所以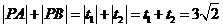 . ------10分
. ------10分
24.解:
(1)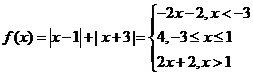 ………..4分
………..4分
则当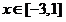 时,
时,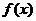 为常函数. ………..5分
为常函数. ………..5分
(2)由柯西不等式得: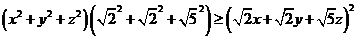
所以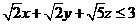
因此M的最大值为3.
数学学习 http://www.yggk.net/math/